Developer Guide and Reference

Download PDF
ID 767253
Date 10/31/2024
Public
Document Table of Contents
Document Table of Contents x
Developer Guide and Reference
Developer Guide and Reference x
Intel® oneAPI DPC++/C++ Compiler Introduction Compiler Setup Compiler Reference Compilation Optimization and Programming Compatibility and Portability Notices and Disclaimers
Intel® oneAPI DPC++/C++ Compiler Introduction x
Get Help and Support Related Information
Compiler Setup x
Use the Command Line Use Eclipse Use Microsoft Visual Studio
Use the Command Line x
Specify Component Locations Invoke the Compiler Use the Command Line on Windows File Extensions Use Makefiles for Compilation Use CMake with the Compiler Use Compiler Options Specify Compiler Files Convert Projects to Use a Selected Compiler
Use Eclipse x
Add the Compiler to Eclipse Multiversion Compiler Support Use Cheat Sheets Create a Simple Eclipse Project Makefiles Use Intel Libraries with Eclipse
Use Microsoft Visual Studio x
Create a New Project Use the Intel® oneAPI DPC++/C++ Compiler Select the Compiler Version Specify a Base Platform Toolset Use Property Pages Use Intel® Libraries with Microsoft Visual Studio* Include MPI Support Use Code Coverage in Microsoft Visual Studio* Use Profile Guided Optimization in Microsoft Visual Studio* Optimization Reports in Microsoft Visual Studio* Dialog Box Help
Dialog Box Help x
Use Intel® oneAPI DPC++/C++ Compiler dialog box Hardware Profile-Guided Optimization dialog box Options: Compilers dialog box Options: Intel Libraries for oneAPI dialog box Options: Converter dialog box Options: Optimization Reports dialog box Options: Profile Guided Optimization dialog box Profile Guided Optimization dialog box Options: Code Coverage dialog box Code Coverage dialog box Code Coverage Settings dialog box
Compiler Reference x
C/C++/SYCL Calling Conventions Compiler Options Floating-Point Operations Attributes Intrinsics Libraries Macros Pragmas Syntactic and Semantic Errors
Compiler Options x
Alphabetical Option List General Rules for Compiler Options What Appears in the Compiler Option Descriptions Optimization Options Advanced Optimization Options Code Generation Options Offload Compilation, OpenMP*, and Parallel Processing Options Interprocedural Optimization Options Profile Guided Optimization Options Optimization Report Options Floating-Point Options Inlining Options Output, Debug, and Precompiled Header Options Preprocessor Options Component Control Options Language Options Data Options Compiler Diagnostic Options Compatibility Options Linking or Linker Options Miscellaneous Options Deprecated and Removed Compiler Options Display Option Information Alternate Compiler Options Portability and GCC-Compatible Warning Options
Optimization Options x
fast fbuiltin, Oi foptimize-sibling-calls GF nolib-inline O Od Ofast Os Ot Ox
Advanced Optimization Options x
ffreestanding, Qfreestanding fjump-tables fvec-allow-scalar-stores, Qvec-allow-scalar-stores fvec-peel-loops, Qvec-peel-loops fvec-remainder-loops, Qvec-remainder-loops fvec-with-mask, Qvec-with-mask ipp-link, Qipp-link mno-gather, Qgather- mno-scatter, Qscatter- qactypes, Qactypes qdaal, Qdaal qipp, Qipp qmkl, Qmkl qmkl-ilp64, Qmkl-ilp64 qmkl-sycl-impl, Qmkl-sycl-impl qopt-assume-no-loop-carried-dep, Qopt-assume-no-loop-carried-dep qopt-dword-index-for-array-of-structs, Qopt-dword-index-for-array-of-structs qopt-dynamic-align, Qopt-dynamic-align qopt-for-throughput, Qopt-for-throughput qopt-mem-layout-trans, Qopt-mem-layout-trans qopt-multiple-gather-scatter-by-shuffles, Qopt-multiple-gather-scatter-by-shuffles qopt-prefetch, Qopt-prefetch qopt-prefetch-distance, Qopt-prefetch-distance qopt-prefetch-loads-only, Qopt-prefetch-loads-only qopt-streaming-stores, Qopt-streaming-stores qopt-zmm-usage, Qopt-zmm-usage qtbb, Qtbb unroll, Qunroll vec, Qvec vec-threshold, Qvec-threshold vecabi, Qvecabi
Code Generation Options x
arch ax, Qax EH fasynchronous-unwind-tables fcf-protection, Qcf-protection fdata-sections, Gw fexceptions ffunction-sections, Gy fomit-frame-pointer Gd GR guard Gv m, Qm m64, Qm64 m80387 march masm mauto-arch, Qauto-arch mbranches-within-32B-boundaries, Qbranches-within-32B-boundaries mintrinsic-promote, Qintrinsic-promote momit-leaf-frame-pointer mtune, tune regcall, Qregcall x, Qx xHost, QxHost
Offload Compilation, OpenMP*, and Parallel Processing Options x
device-math-lib fintelfpga fiopenmp, Qiopenmp flink-huge-device-code fno-sycl-libspirv fopenmp fopenmp-concurrent-host-device-compile, Qopenmp-concurrent-host-device-compile fopenmp-declare-target-scalar-defaultmap, Qopenmp-declare-target-scalar-defaultmap fopenmp-device-code-split, Qopenmp-device-code-split fopenmp-device-lib fopenmp-device-link, Qopenmp-device-link fopenmp-max-parallel-link-jobs, Qopenmp-max-parallel-link-jobs fopenmp-offload-mandatory, Qopenmp-offload-mandatory fopenmp-target-buffers, Qopenmp-target-buffers fopenmp-target-default-sub-group-size, Qopenmp-target-default-sub-group-size fopenmp-target-loopopt, Qopenmp-target-loopopt fopenmp-target-simd, Qopenmp-target-simd fopenmp-targets, Qopenmp-targets fsycl fsycl-add-default-spec-consts-image fsycl-allow-device-dependencies fsycl-dead-args-optimization fsycl-device-code-split fsycl-device-lib fsycl-device-obj fsycl-device-only fsycl-early-optimizations fsycl-enable-function-pointers fsycl-esimd-force-stateless-mem fsycl-explicit-simd fsycl-force-target fsycl-fp64-conv-emu fsycl-help fsycl-host-compiler fsycl-host-compiler-options fsycl-id-queries-fit-in-int fsycl-instrument-device-code fsycl-link fsycl-max-parallel-link-jobs fsycl-optimize-non-user-code fsycl-pstl-offload fsycl-rdc fsycl-remove-unused-external-funcs fsycl-targets fsycl-unnamed-lambda fsycl-use-bitcode ftarget-compile-fast ftarget-export-symbols ftarget-register-alloc-mode, Qtarget-register-alloc-mode nolibsycl qopenmp, Qopenmp qopenmp-link qopenmp-simd, Qopenmp-simd qopenmp-stubs, Qopenmp-stubs reuse-exe Wno-sycl-strict Xopenmp-target Xs Xsycl-target
Interprocedural Optimization Options x
flto ipo, Qipo
Profile Guided Optimization Options x
fprofile-dwo-dir fprofile-ml-use fprofile-sample-generate fprofile-sample-use
Optimization Report Options x
qopt-report, Qopt-report qopt-report-file, Qopt-report-file qopt-report-names, Qopt-report-names qopt-report-phase, Qopt-report-phase qopt-report-stdout, Qopt-report-stdout
Floating-Point Options x
ffp-accuracy, Qfp-accuracy ffp-contract fimf-absolute-error, Qimf-absolute-error fimf-accuracy-bits, Qimf-accuracy-bits fimf-arch-consistency, Qimf-arch-consistency fimf-domain-exclusion, Qimf-domain-exclusion fimf-max-error, Qimf-max-error fimf-precision, Qimf-precision fimf-use-svml, Qimf-use-svml fma, Qfma fp-model, fp fp-speculation, Qfp-speculation ftz, Qftz pc, Qpc
Inlining Options x
fgnu89-inline finline finline-functions inline-forceinline, Qinline-forceinline
Output, Debug, and Precompiled Header Options x
c debug (Linux*) debug (Windows*) Fa fasm-blocks Fe Fo Fp fsystem-debug fverbose-asm g gdwarf grecord-gcc-switches gsplit-dwarf o S use-msasm Y- Yc Yu Zi, Z7, ZI
Preprocessor Options x
B C D dD, QdD dM, QdM E EP FI H, QH I idirafter imacros iprefix iquote isystem iwithprefix iwithprefixbefore M, QM MD, QMD MF, QMF MG, QMG MM, QMM MMD, QMMD MQ, QMQ MT, QMT nostdinc++ P TP U undef X
Component Control Options x
Qoption
Language Options x
ansi fno-gnu-keywords fno-operator-names fno-rtti fpermissive fshort-enums fsyntax-only, Zs funsigned-char, J std, Qstd strict-ansi vd vmg x (type option) Zc Zg Zp
Data Options x
fcommon fkeep-static-consts, Qkeep-static-consts fmaintain-32-byte-stack-align, Qmaintain-32-byte-stack-align fmath-errno fpack-struct fpic fpie fstack-protector fstack-security-check fvisibility fzero-initialized-in-bss, Qzero-initialized-in-bss GA Gs GS mcmodel Qlong-double
Compiler Diagnostic Options x
w W Wabi Wall Wcheck-unicode-security Wcomment Wdeprecated Werror, WX Werror-all Wextra-tokens Wformat Wformat-security Wmain Wmissing-declarations Wmissing-prototypes Wpointer-arith Wreorder Wreturn-type Wshadow Wsign-compare Wstrict-aliasing Wstrict-prototypes Wtrigraphs Wuninitialized Wunknown-pragmas Wunused-function Wunused-variable Wwrite-strings
Compatibility Options x
gcc-toolchain vmv
Linking or Linker Options x
F (Windows*) fixed fortlib fuse-ld l L LD link MD MT nodefaultlibs no-intel-lib, Qno-intel-lib nostartfiles nostdlib pie pthread shared shared-intel shared-libgcc static static-intel static-libgcc static-libstdc++ T u (Linux*) v Wa Wl Wp Xlinker Zl
Miscellaneous Options x
dryrun dumpmachine dumpversion fpreview-breaking-changes help MP nologo save-temps, Qsave-temps showIncludes sox sysroot Tc TC Tp version
Floating-Point Operations x
Programming Tradeoffs in Floating-Point Applications Floating-Point Optimizations Denormal Numbers Floating-Point Environment Set the FTZ and DAZ Flags Tuning Performance IEEE Floating-Point Operations
Attributes x
align align_value allow_cpu_features code_align const cpu_dispatch, cpu_specific target
Libraries x
Create Libraries Use Intel Shared Libraries Manage Libraries Redistribute Libraries When Deploying Applications Resolve References to Shared Libraries Redistributable Library Considerations Intel's Memory Allocator Library SIMD Data Layout Templates Intel® C++ Class Libraries Intel's C++ Asynchronous I/O Extensions for Windows IEEE 754-2008 Binary Floating-Point Conformance Library Intel's Numeric String Conversion Library
SIMD Data Layout Templates x
Function Calls and Containers User-Level Interface Examples
Function Calls and Containers x
Construct an n_container Bounds
User-Level Interface x
SDLT Primitives soa1d_container aos1d_container n_container Bounds Accessors Proxy Objects Number Representation Indexes Convenience and Correctness
aos1d_container x
access_by
n_container x
Layouts Shape make_ n_container template function extent_d template function
Shape x
n_extent_generator
Bounds x
bounds_t sdlt::bounds Template Function n_bounds_t n_bounds_generator bounds_d Template Function
Accessors x
soa1d_container::accessor and aos1d_container::accessor soa1d_container::const_accessor and aos1d_container::const_accessor Accessor Concept
Proxy Objects x
Proxy ConstProxy
Number Representation x
aligned_offset fixed_offset
Indexes x
linear_index n_index_t n_index_generator index_d template function
Convenience and Correctness x
max_val min_val
Examples x
Efficiency with Structure of Arrays Example Complex SDLT Primitive Construction Example Forward Dependency Example Use of Offsets and Methods on a SDLT Primitive Example RGB to YUV Conversion Example
Intel® C++ Class Libraries x
C++ Classes and SIMD Operations Capabilities of C++ SIMD Classes Integer Vector Classes Floating-Point Vector Classes Classes Quick Reference Programming Example Intel's valarray Implementation
Integer Vector Classes x
Terms and Syntax Rules for Operators Assignment Operator Logical Operators Addition and Subtraction Operators Multiplication Operators Shift Operators Comparison Operators Conditional Select Operators Debug Operations Unpack Operators Pack Operators Clear MMX™ State Operator Integer Functions for Intel® Streaming SIMD Extensions Conversions between Fvec and Ivec
Floating-Point Vector Classes x
Fvec Syntax and Notation Data Alignment Conversions Constructors and Initialization Arithmetic Operators Minimum and Maximum Operators Logical Operators Compare Operators Conditional Select Operators for Fvec Classes Cacheability Support Operators Debug Operations Load and Store Operators Unpack Operators Move Mask Operators
Intel's C++ Asynchronous I/O Extensions for Windows x
Intel's C++ Asynchronous I/O Library for Windows Intel's C++ Asynchronous I/O Class for Windows
Intel's C++ Asynchronous I/O Library for Windows x
aio_read aio_write Example for aio_read and aio_write Functions aio_suspend Example for aio_suspend Function aio_error aio_return Example for aio_error and aio_return Functions aio_fsync aio_cancel Example for aio_cancel Function lio_listio Example for lio_listio Function Asynchronous I/O Function Errors
Intel's C++ Asynchronous I/O Class for Windows x
Template Class async_class get_last_operation_id wait get_status get_last_error get_error_operation_id stop_queue resume_queue clear_queue Example for Using async_class Template Class
IEEE 754-2008 Binary Floating-Point Conformance Library x
Intel® IEEE 754-2008 Binary Floating-Point Conformance Library and Usage Function List Homogeneous General-Computational Operations Functions General-Computational Operation Functions Quiet-Computational Operations Functions Signaling-Computational Operations Functions Non-Computational Operations Functions
Intel's Numeric String Conversion Library x
Use Intel's Numeric String Conversion Library Function List
Macros x
ISO Standard Predefined Macros Additional Predefined Macros Use Predefined Macros to Specify Intel® Compilers
Pragmas x
Intel-Specific Pragma Reference Supported OpenMP* Pragmas Pragmas Compatible with Other Compilers
Intel-Specific Pragma Reference x
block_loop/noblock_loop distribute_point inline, noinline, forceinline ivdep loop_count nofusion novector omp target variant dispatch ompx prefetch data prefetch/noprefetch unroll/nounroll unroll_and_jam/nounroll_and_jam vector
Compilation x
Compilation Overview Supported Environment Variables Pass Options to the Linker Specify Alternate Tools Use Configuration Files Use Response Files Global Symbols and Visibility Attributes for Linux* Save Compiler Information in Your Executable Link Debug Information Ahead of Time Compilation Device Offload Compilation Considerations Use a Third-Party Compiler as a Host Compiler for SYCL Code
Optimization and Programming x
OpenMP* Support SYCL* Support Compiler Sanitizers Intel® oneAPI Level Zero Vectorization Instrumented Profile-Guided Optimization Hardware Profile-Guided Optimization High-Level Optimization Interprocedural Optimization Methods to Optimize Code Size Optimization Reports Compiler Math Library SYCL* Device Library
OpenMP* Support x
Add OpenMP* Support Parallel Processing Model Worksharing Using OpenMP* Control Thread Allocation OpenMP* Library Support OpenMP* Contexts OpenMP* Offloading SPMD/SIMT and SIMD Models OpenMP* Advanced Issues OpenMP* Implementation-Defined Behaviors OpenMP* Examples
OpenMP* Library Support x
OpenMP* Runtime Library Routines Intel® Compiler Extension Routines to OpenMP* OpenMP* Support Libraries Use the OpenMP* Libraries Thread Affinity Interface OpenMP* Memory Spaces and Allocators
OpenMP* Contexts x
OpenMP* Context Selectors Score and Match Context Selectors
SYCL* Support x
SYCL* Extensions Redistribute Your SYCL* Application CUDA* to SYCL* Migration
Intel® oneAPI Level Zero x
Intel® oneAPI Level Zero Switch Intel® oneAPI Level Zero Backend Specification Programming with the Intel® oneAPI Level Zero Backend
Vectorization x
Automatic Vectorization Explicit Vector Programming
Automatic Vectorization x
Vectorization Programming Guidelines Use Automatic Vectorization Vectorization and Loops Loop Constructs
Explicit Vector Programming x
User-Mandated or SIMD Vectorization SIMD-Enabled Functions SIMD-Enabled Function Pointers Function Annotations and the SIMD Directive for Vectorization Explicit SIMD SYCL Extension
Interprocedural Optimization x
Use Interprocedural Optimization Performance Considerations Create a Library from IPO Objects Inline Expansion of Functions
Compiler Math Library x
Use the Compiler Math Library Math Function List Trigonometric Functions Hyperbolic Functions Exponential Functions Special Functions Nearest Integer Functions Remainder Functions Miscellaneous Functions Complex Functions C99 Macros
SYCL* Device Library x
Basic Arithmetic Operations and Simple Math Functions IMF Transcendental Math Functions
Basic Arithmetic Operations and Simple Math Functions x
Simple Integer Math Functions Basic Integer Arithmetic Operations Simple Arithmetic Operations with Rounding Mode Type Casting Functions for Floating-Point Numbers Type Casting Functions for Half-Precision Types Type Casting Functions for bfloat16 Type Simple Half-Precision Arithmetic Math Functions Half-Precision Comparison Functions
IMF Transcendental Math Functions x
IMF Device Library Usage Example IMF Device Library Function List IMF Device Library Trigonometric Functions IMF Device Library Hyperbolic Functions IMF Device Library Exponential Functions IMF Device Library Logarithmic Functions IMF Device Library Power Functions IMF Device Library Special Functions cdfnorm cdfnorminv cyl_bessel_i0 cyl_bessel_i1 erf erfc erfcinv erfcx erfinv j0 j1 jn lgamma tgamma y0 y1 yn IMF Device Library Rounding Functions IMF Device Library Miscellaneous Functions
Compatibility and Portability x
Standards Conformance GCC Compatibility and Interoperability Microsoft Compatibility Port from Microsoft Visual C++* to the Intel® oneAPI DPC++/C++ Compiler Port from GCC* to the Intel® oneAPI DPC++/C++ Compiler
Port from Microsoft Visual C++* to the Intel® oneAPI DPC++/C++ Compiler x
Modify Your makefile Other Considerations
Port from GCC* to the Intel® oneAPI DPC++/C++ Compiler x
Modify Your makefile Other Considerations
Developer Guide and Reference

IMF Device Library Special Functions

The IMF Device Library supports the following special functions and their inverses:

cdfnorm

Description: The cdfnorm(x) function returns the cumulative normal distribution function value of x.

This function is a useful one for Monte Carlo applications in computational finance.

Special Values:

Argument x Result cdfnorm(x)
-∞ +0
x < UDFL +0
+∞ +1
NOTE:
UDFL is the underflow threshold. UDFL = ~ -14.2 for float, ~ -38.5 for double precisions.

Useful Identities:

cdfnorm(x) = 1/2 · ( 1 + erf( x/sqrt(2) ) )
cdfnorm(x) = 1 - 1/2 · erfc( x/sqrt(2) )

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::cdfnorm ( float x );
double      sycl::ext::intel::math::cdfnorm ( double x );

// CUDA-specific naming for the same functions
float       sycl::ext::intel::math::cdfnorm ( float x );
double      sycl::ext::intel::math::cdfnorm ( double x );

cdfnorminv

Description: The cdfnorminv(x) function returns the inverse cumulative normal distribution function value of x.

This function is a useful one for Monte Carlo applications in computational finance.

Special Values:

Argument x Result cdfnorminv(x)
-∞ QNAN
x < -0 QNAN
+/-0 -∞
+0.5 +0
+1 +∞
x > +1 QNAN
+∞ QNAN

Useful Identities:

cdfnorminv(x) = sqrt(2) · erfinv( 2·x - 1 )
cdfnorminv(x) = sqrt(2) · erfcinv( 2 - 2·x )

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::cdfnorminv ( float x );
double      sycl::ext::intel::math::cdfnorminv ( double x );

// CUDA-specific naming for the same functions
float       sycl::ext::intel::math::normcdfinv ( float x );
double      sycl::ext::intel::math::normcdfinv ( double x );

cyl_bessel_i0

Description: The cyl_bessel_i0(x) function returns the value of the regular modified cylindrical Bessel function of an order of 0 for the input argument x.

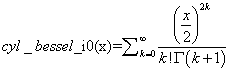
Special Values:

Argument x Result cyl_bessel_i0(x)
-∞ +∞
+/-0 +1
+∞ +∞

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::cyl_bessel_i0 ( float x );
double      sycl::ext::intel::math::cyl_bessel_i0 ( double x );

cyl_bessel_i1

Description: The cyl_bessel_i1(x) function returns the value of the regular modified cylindrical Bessel function of an order of 1 for the input argument x.

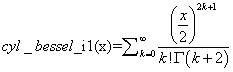
Special Values:

Argument x Result cyl_bessel_i1(x)
-∞ -∞
+/-0 +/-0
+∞ +∞

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::cyl_bessel_i1 ( float x );
double      sycl::ext::intel::math::cyl_bessel_i1 ( double x );

erf

Description: The erf(x) function returns the error function value of x.

Special Values:

Argument x Result erf(x)
-∞ -1
+∞ +1

Useful Identities:

erf(x) = 1 - erfc(x)

Calling Interfaces:

  • Default accuracy: 
    float       sycl::ext::intel::math::erf ( float x );
double      sycl::ext::intel::math::erf ( double x );
  • High accuracy (HA): 
    float       sycl::ext::intel::math::ha::erf ( float x );
double      sycl::ext::intel::math::ha::erf ( double x );
  • Low accuracy (LA): 
    float       sycl::ext::intel::math::la::erf ( float x );
double      sycl::ext::intel::math::la::erf ( double x );
  • Enhanced performance: 
    float       sycl::ext::intel::math::ep::erf ( float x );
double      sycl::ext::intel::math::ep::erf ( double x );

erfc

Description: The erfc(x) function returns the complementary error function value of x: 1 - erf(x)

This function is useful when erf(x) is close to 1 to obtain greater accuracy.

Special Values:

Argument x Result erfc(x)
-∞ +2
x > UDFL +0
+∞ +0
NOTE:
UDFL is underflow threshold. UDFL = ~9.2 for float, ~26.6 for double precisions.

Useful Identities:

erfc(x) = 1 - erf(x)

Calling Interfaces:

  • Default accuracy: 
    float       sycl::ext::intel::math::erfc ( float x );
double      sycl::ext::intel::math::erfc ( double x );
  • High accuracy (HA): 
    float       sycl::ext::intel::math::ha::erfc ( float x );
double      sycl::ext::intel::math::ha::erfc ( double x );
  • Low accuracy (LA): 
    float       sycl::ext::intel::math::la::erfc ( float x );
double      sycl::ext::intel::math::la::erfc ( double x );

erfcinv

Description: The erfcinv(x) function returns the inverse complementary error function value of x: erfinv(1-x).

The inverse complementary error function is useful for Monte Carlo applications in computational finance as it is closely related to the normal cumulative distribution. Use the erfcinv(x) function to replace expressions containing erfinv(1-x) for greater accuracy when x is close to 1.

Special Values:

Argument x Result erfcinv(x)
-∞ QNAN
x < -0 QNAN
+/-0 +∞
+1 +0
+2 -∞
x > +0 QNAN
+∞ QNAN

Useful Identities:

erfcinv(x) = erfinv(1-x)

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::erfcinv ( float x );
double      sycl::ext::intel::math::erfcinv ( double x );

erfcx

Description: The erfcx(x) function returns the scaled complementary error function value of x: exp(x^2)·erfc(x).

This computation sequence occurs in diffusion problems of physics and chemistry and may be useful to avoid underflow and overflow errors computing exp(x^2) and erfc(x) separately.

Special Values:

Argument x Result erfcx(x)
-∞ +∞
+∞ +0

Useful Identities:

erfcx(x) ~ (1/sqrt(π))/x, for large x

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::erfcx ( float x );
double      sycl::ext::intel::math::erfcx ( double x );

erfinv

Description: The erfinv(x) function returns the inverse error function value of x.

The inverse error function is useful for Monte Carlo applications in computational finance as it is closely related to the normal cumulative distribution.

Special Values:

Argument x Result erfinv(x)
-∞ QNAN
+/-0 +/-0
+/-1 +/-∞
|x| > 1 QNAN
+∞ QNAN

Useful Identities:

erfinv(x) = erfcinv(1-x)

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::erfinv ( float x );
double      sycl::ext::intel::math::erfinv ( double x );

j0

Description: The j0(x) function returns the value of the Bessel function of the first kind of order 0 for the input argument x.

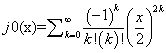
Special Values:

Argument x Result j0(x)
-∞ +0
+/-0 +1
+∞ +0

Calling Interfaces:Default accuracy: 

float       sycl::ext::intel::math::j0 ( float x );
double      sycl::ext::intel::math::j0 ( double x );

j1

Description: The j1(x) function returns the value of the Bessel function of the first kind of order 1 for the input argument x.

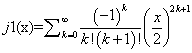
Special Values:

Argument x Result j1(x)
-∞ +0
+/-0 +/-0
+∞ +0

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::j1 ( float x );
double      sycl::ext::intel::math::j1 ( double x );

jn

Description: The jn(n,x) function returns the value of the Bessel function of the first kind of given order n for the input argument x.

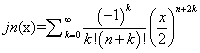
Special Values:

Argument n Argument x Result jn(n,x)
any -∞ +0
0 +/-0 +1
n >= 1 +/-0 +/-0
any +∞ +0

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::jn ( int n, float x );
double      sycl::ext::intel::math::jn ( int n, double x );

lgamma

Description: The lgamma(x) function returns the value of the natural logarithm of the absolute value of gamma: log( |tgamma(x)| ).

Special Values:

Argument x Result lgamma(x)
-∞ +∞
neg, int +∞
+/-0 +∞
+1 +0
+2 +0
+∞ +∞

Useful Identities:

lgamma(x) = log(|tgamma(x)|), less accurate and impacted by overflows in tgamma

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::lgamma ( float x );
double      sycl::ext::intel::math::lgamma ( double x );

tgamma

Description: The tgamma(x) function returns the gamma function value of x.

Special Values:

Argument x Result tgamma(x)
-∞ QNAN
neg, int QNAN
+/-0 +/-∞
x > OVFL +∞
+∞ +∞
NOTE:
OVFL is the overflow threshold. OVFL = ~ 35.1 for float, ~ 171.7 for double precisions.

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::tgamma ( float x );
double      sycl::ext::intel::math::tgamma ( double x );

y0

Description: The y0(x) function returns the value of the Bessel function of the second kind of order 0 for the input argument x.

Special Values:

Argument x Result y0(x)
-∞ QNAN
x < +0 QNAN
+/-0 -∞
+∞ +0

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::y0 ( float x );
double      sycl::ext::intel::math::y0 ( double x );

y1

Description: The y1(x) function returns the value of the Bessel function of the second kind of order 1 for the input argument x.

Special Values:

Argument x Result y0(x)
-∞ QNAN
x < +0 QNAN
+/-0 -∞
+∞ +0

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::y1 ( float x );
double      sycl::ext::intel::math::y1 ( double x );

yn

Description: The yn(n,x) function returns the value of the Bessel function of the second kind of given order n for the input argument x.

Special Values:

Argument n Argument x Result yn(n,x)
any -∞ QNAN
any x < +0 QNAN
any +/-0 -∞
any +∞ +0

Calling Interfaces:

Default accuracy: 

float       sycl::ext::intel::math::yn ( int n, float x );
double      sycl::ext::intel::math::yn ( int n, double x );

Parent topic: IMF Transcendental Math Functions
Level Two Title