Developer Guide and Reference for Intel® Cryptography Primitives Library
A newer version of this document is available. Customers should click here to go to the newest version.
Visible to Intel only — GUID: GUID-D3ADFC8D-428B-41C6-8E8B-5D2FF822F443
Visible to Intel only — GUID: GUID-D3ADFC8D-428B-41C6-8E8B-5D2FF822F443
Prime Number Generation Functions
This section introduces Intel® Cryptography Primitives Library functions for prime number generation.
This section describes Intel® Cryptography Primitives Library functions for generating probable prime numbers of variable lengths and validating probable prime numbers through a probabilistic primality test scheme for cryptographic use. A probable prime number is thus defined as an integer that passes the Miller-Rabin probabilistic primality-based test.
The scheme adopted for the probable prime number generation is based on a well-known prime number theorem. Study shows that the number of primitives that are no greater than the given large integer x is closely approximated by the expression. Let π(x) denote the number of primes that are not greater than x. In this case the statement is true 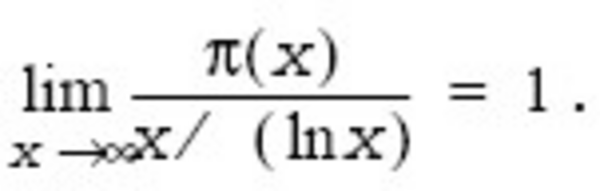
Further study indicates that if X represents the event where the tested k-bit integer n is composite and if Yt denotes the event where the Miller-Rabin test with the security parameter t declares n to be a prime, the test error probability is upper bounded by 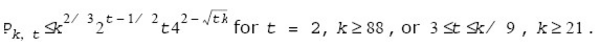
Subsequently, a practical strategy for generating a random k-bit probable prime is to repeatedly pick k-bit random odd integers until finding one integer that can pass a recognized probabilistic primality test scheme as a probable prime. The available set of probable prime number generation functions enables you to specify an appropriate value of the security parameter t used in the Miller-Rabin primality test to meet the cryptographic requirements for your application.
All Intel® Cryptography Primitives Library for prime number generation use the context IppsPrimeState as an operational vehicle that carries the bitlength of the target probable prime number, the structure capturing the state of the pseudorandom number generation, the structured working buffer used for Montgomery modular computation in the Miller-Rabin primality test, and the buffer to store the generated probable prime number.
The following sequence of operations is required to generate a probable prime number of the specified bitlength:
Call the function PrimeGetSize to get the size required to configure the IppsPrimeState context.
Allocate memory through the operating system memory allocation function and configure the IppsPrimeState context by calling the functionPrimeInit.
Generate a probable prime number of the specified bitlength by calling the function PrimeGen_BN. If the returned IppStatus is ippStsInsufficientEntropy, then change the parameters of the pseudorandom generator and call the function PrimeGen_BN again.
Clean up secret data stored in the context.
Free the memory allocated to the IppsPrimeState context by calling the operating system memory-free service function.
Related Information