Application Notes for oneMKL Summary Statistics

Download PDF
ID 772991
Date 3/31/2023
Public
Document Table of Contents
Document Table of Contents x
Application Notes for Intel® oneAPI Math Kernel Library Summary Statistics
Application Notes for Intel® oneAPI Math Kernel Library Summary Statistics x
Legal Information About This Document About Summary Statistics Algorithms and Interfaces in Summary Statistics Common Usage Model of Summary Statistics Algorithms Processing Data in Blocks Detecting Outliers in Datasets Dealing with Missing Observations Computing Quantiles for Streaming Data Bibliography
About This Document x
Conventions and Symbols
Algorithms and Interfaces in Summary Statistics x
Estimating Raw and Central Moments and Sums, Skewness, Excess Kurtosis, Variation, and Variance-Covariance/Correlation/Cross-Product Matrix Computing Median Absolute Deviation Computing Mean Absolute Deviation Computing Minimum/Maximum Values Calculating Order Statistics Estimating Quantiles Estimating a Pooled/Group Variance-Covariance Matrices/Means Estimating a Partial Variance-Covariance Matrix Performing Robust Estimation of a Variance-Covariance Matrix Detecting Multivariate Outliers Handling Missing Values in Matrices of Observations Parameterizing a Correlation Matrix Sorting an Observation Matrix
Estimating Raw and Central Moments and Sums, Skewness, Excess Kurtosis, Variation, and Variance-Covariance/Correlation/Cross-Product Matrix x
Computing Estimations for Large Datasets Calculating Multiple Estimates
Estimating Quantiles x
Computing Quantiles for Streaming Data with VSL_SS_METHOD_SQUANTS_ZW
Handling Missing Values in Matrices of Observations x
Basic Assumptions for the MI Method Basic Components of the MI Method
Detecting Outliers in Datasets x
Using the BACON Algorithm for Outlier Detection Using Robust Methods
Application Notes for Intel® oneAPI Math Kernel Library Summary Statistics

Estimating a Partial Variance-Covariance Matrix

Use the VSL_SS_FAST_METHOD method to compute a partial variance-covariance matrix.

For the definition of a partial variance-covariance matrix, see the Mathematical Notation and Definitions chapter in the Summary Statistics section of [MKLMan].

To calculate the matrix, provide a variance-covariance matrix and split the random vector ξ = (ξ1,...,ξ7) of dimension p into two non-overlapping sub-components, Υ and Ζ. Each component is encoded as follows:

, for all i = 1,...,p.

This partition defines the following structure of the variance-covariance matrix:

.

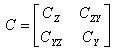Partial variance-covariance is calculated as: P = CΥ - CΥΖCΖ-1CΖΥ.

The example below demonstrates computation of a partial variance-covariance matrix: 

#include "mkl.h"
 
#define N          1000     /* number of observations */
#define DIM           4     /* dimension of the task */
#define PART_DIM (DIM/2)    /* dimension of partial variance-covariance */
 
int main()
{
    int i, j, status;
    VSLSSTaskPtr task;
    MKL_INT p, n, xstorage, covstorage, pcovstorage;
    double x[DIM][N];  /* matrix of observations */
    unsigned long long estimates;
 
    double mean[DIM], cov[DIM][DIM];
    MKL_INT p_index[DIM];
    double p_cov[PART_DIM][PART_DIM];
 
    p = DIM;
    n = N;
    xstorage    = VSL_SS_MATRIX_STORAGE_ROWS;
    covstorage  = VSL_SS_MATRIX_STORAGE_FULL;
    pcovstorage = VSL_SS_MATRIX_STORAGE_FULL;
 
    /* Splitting random vector into two components */
    for(i=0;i<DIM;i++)
    {
        p_index[i]=(i<PART_DIM)? 1 : -1;
        mean[i] = 0.0;
        for(j=0;j<DIM;j++) cov[i][j]=0;
    }
 
    for(i=0;i<PART_DIM;i++)
    {
        for(j=0;j<PART_DIM;j++) p_cov[i][j]=0;
    }
 
    /* Create a task */
    status = vsldSSNewTask( &task, &p, &n, &xstorage, x, 0, 0 );
 
    /* Initialize the task parameters */
    status = vsldSSEditCovCor( task, mean, cov, &covstorage, 0, 0 );
    status = vsldSSEditPartialCovCor( task, p_index, cov, &covstorage,
                                      0, 0, p_cov, &pcovstorage, 0, 0 );  
 
    /* Compute the variance-covariance and partial variance-covariance matrices */
    estimates = VSL_SS_COV | VSL_SS_PARTIAL_COV;
    status = vsldSSCompute( task, estimates, VSL_SS_METHOD_FAST );
 
    /* Deallocate the task resources */
    status = vslSSDeleteTask( &task );
 
    return 0;
}
Parent topic: Algorithms and Interfaces in Summary Statistics
Level Two Title