Intel® oneAPI Math Kernel Library Cookbook

Download PDF
ID 758503
Date 6/24/2024
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Intel® oneAPI Math Kernel Library Cookbook
Intel® oneAPI Math Kernel Library Cookbook x
Notices and Disclaimers Getting Technical Support What's New Notational Conventions Related Information Finding an approximate solution to a stationary nonlinear heat equation Factoring general block tridiagonal matrices Solving a system of linear equations with an LU-factored block tridiagonal coefficient matrix Factoring block tridiagonal symmetric positive definite matrices Solving a system of linear equations with a block tridiagonal symmetric positive definite coefficient matrix Computing principal angles between two subspaces Computing principal angles between invariant subspaces of block triangular matrices Evaluating a Fourier integral Using Fast Fourier Transforms for computer tomography image reconstruction Noise filtering in financial market data streams Using the Monte Carlo method for simulating European options pricing Using the Black-Scholes formula for European options pricing Multiple simple random sampling without replacement Using a histospline technique to scale images Speeding up Python* scientific computations Bibliography
Intel® oneAPI Math Kernel Library Cookbook

Solving a system of linear equations with an LU-factored block tridiagonal coefficient matrix

Goal

Use oneMKL LAPACK routines to craft a solution to a system of equations involving a block tridiagonal matrix, since LAPACK does not have routines that directly solve systems with block tridiagonal matrices.

Solution

oneMKL LAPACK provides a wide range of subroutines for solving systems of linear equations with an LU-factored coefficient matrix. It covers dense matrices, band matrices and tridiagonal matrices. This recipe extends this set to block tridiagonal matrices subject to condition all the blocks are square and have the same order. A block triangular matrix A has the form


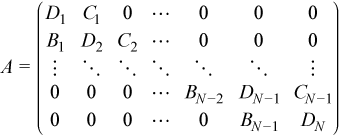
Solving a system AX=F with an LU-factored matrix A=LU and multiple right hand sides (RHS) consists of two stages (see Factoring General Block Tridiagonal Matrices for LU factorization).

  1. Forward substitution, which consists of solving a system of equations LY=F with pivoting, where L is a lower triangular coefficient matrix. For factored block tridiagonal matrices, all blocks of Y except the last one can be found in a loop which consists of

    1. Applying pivoting permutations locally to the right hand side.

    2. Solving the local system of NB linear equations with a lower triangular coefficient matrix, where NB is the order of the blocks.

    3. Updating the right hand side for the next step.

    The last two block components are found outside of the loop because of the structure of the final pivoting (two block permutations need to be applied consecutively) and the structure of the coefficient matrix.

  2. Backward substitution, which consists of solving the system UX=Y. This step is simpler because it does not involve pivoting. The procedure is similar to the first step:

    1. Solving systems with triangular coefficient matrices.

    2. Updating right hand side blocks.

    The difference from the previous step is that the coefficient matrix is upper, not lower, triangular, and the direction of the loop is reversed.

Source code: see the BlockTDS_GE/source/dgeblttrs.f file in the samples archive available at https://www.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip. See also /block_lu_decomposition on GitHub.

Forward Substitution

! Forward substitution
! In the loop compute components Y_K stored in array F
      DO K = 1, N-2
          DO I = 1, NB
              IF (IPIV(I,K) .NE. I) THEN
                  CALL DSWAP(NRHS, F((K-1)*NB+I,1), LDF, F((K-1)*NB+IPIV(I,K),1), LDF)
              END IF
          END DO
          CALL DTRSM('L', 'L', 'N', 'U', NB, NRHS, 1D0, D(1,(K-1)*NB+1), NB, F((K-1)*NB+1,1), LDF)
          CALL DGEMM('N', 'N', NB, NRHS, NB, -1D0, DL(1,(K-1)*NB+1), NB, F((K-1)*NB+1,1), LDF, 1D0, 
     +        F(K*NB+1,1), LDF)
      END DO

! Apply two last pivots     
      DO I = 1, NB
           IF (IPIV(I,N-1) .NE. I) THEN
               CALL DSWAP(NRHS, F((N-2)*NB+I,1), LDF, F((N-2)*NB+IPIV(I,N-1),1), LDF)
           END IF
      END DO

      DO I = 1, NB
           IF(IPIV(I,N)-NB.NE.I)THEN
               CALL DSWAP(NRHS, F((N-1)*NB+I,1), LDF, F((N-2)*NB+IPIV(I,N),1), LDF)
           END IF
      END DO
! Computing Y_N-1 and Y_N out of loop and store in array F     
      CALL DTRSM('L', 'L', 'N', 'U', NB, NRHS, 1D0, D(1,(N-2)*NB+1), NB, F((N-2)*NB+1,1), LDF)
      CALL DGEMM('N', 'N', NB, NRHS, NB, -1D0, DL(1,(N-2)*NB +1), NB, F((N-2)*NB+1,1), LDF, 1D0, 
     +     F((N-1)*NB+1,1), LDF)

Backward Substitution

      …
! Backward substitution
! Computing X_N out of loop and store in array F
      CALL DTRSM('L', 'U', 'N', 'N', NB, NRHS, 1D0, D(1,(N-1)*NB+1), NB, F((N-1)*NB+1,1), LDF)
! Computing X_N-1 out of loop and store in array F
      CALL DGEMM('N', 'N', NB, NRHS, NB, -1D0, DU1(1,(N-2)*NB +1), NB, F((N-1)*NB+1,1), LDF, 1D0, 
     +    F((N-2)*NB+1,1), LDF)
      CALL DTRSM('L', 'U', 'N', 'N', NB, NRHS, 1D0, D(1,(N-2)*NB+1), NB, F((N-2)*NB+1,1), LDF)
! In the loop computing components X_K stored in array F      
      DO K = N-2, 1, -1
          CALL DGEMM('N','N',NB, NRHS, NB, -1D0, DU1(1,(K-1)*NB +1), NB, F(K*NB+1,1), LDF, 1D0, 
     +        F((K-1)*NB+1,1), LDF)
          CALL DGEMM('N','N',NB, NRHS, NB, -1D0, DU2(1,(K-1)*NB +1), NB, F((K+1)*NB+1,1), LDF, 1D0, 
     +        F((K-1)*NB+1,1), LDF)
          CALL DTRSM('L', 'U', 'N', 'N', NB, NRHS, 1D0, D(1,(K-1)*NB+1), NB, F((K-1)*NB+1,1), LDF)
      END DO      
      …

Routines Used

Task

Routine

Description

Apply pivoting permutations

dswap

Swap a vector with another vector

Solve a system of linear equations with lower and upper triangular coefficient matrices

dtrsm

Solve a triangular matrix equation

Update the right hand side blocks

dgemm

Compute a matrix-matrix product with general matrices.

Discussion

NOTE:

A general block tridiagonal matrix with blocks of size NB by NB can be treated as a band matrix with bandwidth 4*NB-1 and solved by calling oneMKL LAPACK subroutines for factoring and solving band matrices (?gbtrf and ?gbtrs). But using the approach described in this recipe requires fewer floating point computations because if the block matrix is stored as a band matrix, many zero elements would be treated as nonzeros in the band and would be processed during computations. The effect increases for bigger NB. Analogously, band matrices can also be treated as block tridiagonal matrices. But this storage scheme is also not very efficient because the blocks would contain many zeros treated as nonzeros. So band storage schemes and block tridiagonal storage schemes and their respective solvers should be considered as complementary to each other.

Given a system of linear equations:


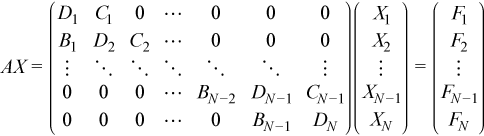
The block tridiagonal coefficient matrix A is assumed to be factored as shown:


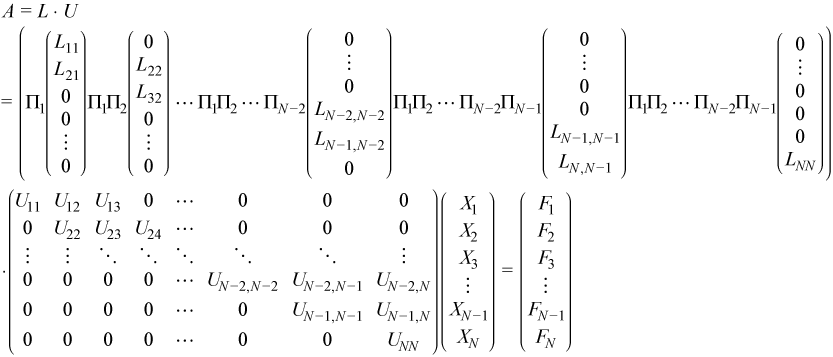
See Factoring General Block Tridiagonal Matrices for a definition of the terms used.

The system is decomposed into two systems of linear equations:


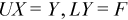
The second equation can be expanded:


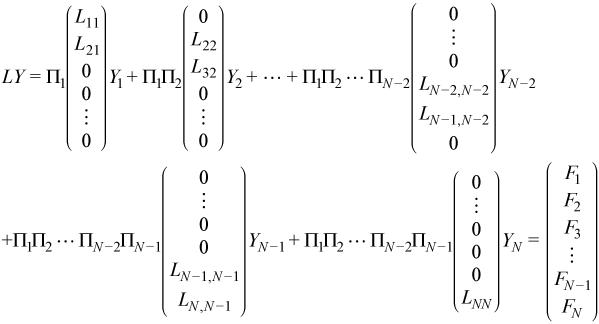
In order to find Y1, first the permutation Π1T must be applied. This permutation only changes the first two blocks of the right hand side:


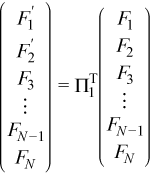
Applying the permutation locally gives


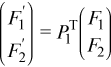
Now Y1 can be found:


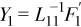
After finding Y1, similar computations can be repeated to find Y2, Y3, ..., and YN - 2.

NOTE:

The different structure of ΠN - 1 (see Factoring General Block Tridiagonal Matrices) means that the same equations cannot be used to compute YN - 1 and YN and that they must be computed outside of the loop.

The algorithm to use the equations to find Y is: 

do for k = 1 to N - 2
    
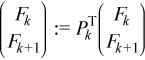
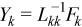                //using ?trsm
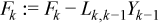        //update right hand side using ?gemm
end do

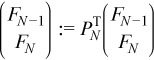
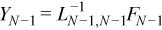      //?trsm
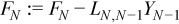    //update right hand side using ?gemm
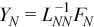             //?trsm

The UX = Y equations can be represented as


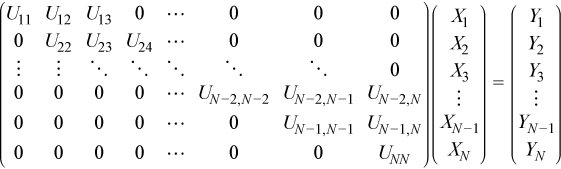
The algorithm for solving these equations is: 

                         //?trsm
   //?gemm followed by ?trsm
do for k = N - 1 to 1 in steps of -1
                  //?gemm
                  //?gemm
                          //?trsm
end do
Parent topic: Intel® oneAPI Math Kernel Library Cookbook
Level Two Title