Introduction
The QR decomposition of a matrix is an essential kernel for a variety of problems in scientific computing. It can be used to find a solution of a linear system, solve linear least squares or eigenvalue problems, estimate the rank of the matrix, and many other numerical linear algebra problems. These are just several important examples arising from various applications.
Intel® Math Kernel Library (Intel® MKL) version 2019 introduces Sparse QR Solver. Intel® MKL Sparse QR [1] is a multifrontal sparse QR factorization method that relies on the processing of blocks of rows. The solver uses nested dissection ordering technique to reduce the fill-in of the factor R. The efficiency of its parallel implementation allows for this choice of ordering algorithm. In addition, the initial matrices can be represented in a form that is more suitable for parallel QR factorization. External interfaces for the Sparse QR functionality are aligned with the Inspector-Executor API for Sparse BLAS [2], which allows them to be used together with no additional efforts from the user. The Sparse QR Solver also uses Intel ® MKL BLAS Level 3 [3] functionality during the factorization of the frontal matrix to achieve the best performance in the numerical factorization stage.
Product Overview
Following the general concept of sparse direct methods, the whole algorithm is divided into three steps:
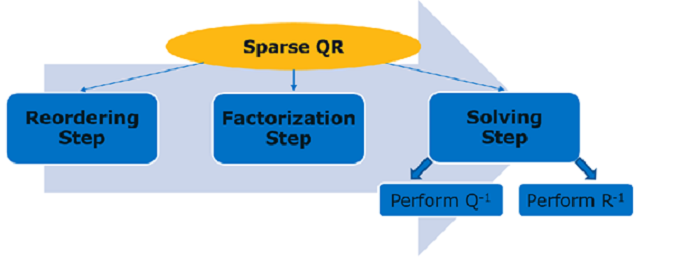
- Reordering step: During this stage, the ordering, structure analysis and symbolic factorization will be performed.
- Factorization step: This is essentially a numerical factorization of the matrix.
- Solving step: In the final stage, the factorization is used to compute the solution of a sparse linear system.
It’s also worth noting, that dividing the problem into stages allows one to reuse data obtained from the first step, for instance if dealing with several matrix systems that have identical non-zero pattern but different numerical values.
Consider a sparse rectangular matrix A of size M-by-N. The matrix A is stored in a compressed sparse row (CSR) storage format (e.g. pointerB, pointerE, columns and values arrays [4]) with zero-based indexing. Let us denote by b, our right-hand side vector. In order to find the solution vector x for this system of equations (i.e. Ax = b), one should invoke the Intel ® MKL routines in the following order (the example uses double precision):
First, we need to create a data structure, csrA (we call this a sparse handle) to store the sparse matrix data in a format that can be passed to both Sparse QR and IE SpBLAS functionality.
mkl_sparse_d_create_csr (&csrA, SPARSE_INDEX_BASE_ZERO, M, N, pointerB, pointerE, columns, values);
Second, call the reordering step of Sparse QR with appropriate descriptor, descrA = {.type = SPARSE_MATRIX_TYPE_GENERAL}:
mkl_sparse_d_qr_reorder (csrA, descrA);
Third, call the factorization step of Sparse QR. Here alt_values (a double precision array) can be added in order to perform the factorization with a matrix, which values are different from the initial matrix A but that has the same sparsity pattern. If NULL vector is passed for alt_values, the original values data in csrA is used in the factorization.
mkl_sparse_d_qr_factorize (csrA, alt_values);
Fourth, call the solving step of Sparse QR. The x and b can be either vectors or dense matrices. So, one should specify the storage order (row-major or column major) and sizes.
mkl_sparse_d_qr_solve( SPARSE_OPERATION_NON_TRANSPOSE, csrA, alt_values,
SPARSE_LAYOUT_COLUMN_MAJOR, 1, x, N, b, M );
Finally, once we are finished using the sparse handle, csrA, in SparseQR or IE Sparse BLAS routines, call
mkl_sparse_destroy(csrA) ;
to release the memory.
The Intel ® MKL Sparse QR implementation includes both Fortran and C interfaces. Currently, Sparse QR supports only real data types, with single or double precision arithmetic.
For more details, please refer to the documentation in [1] and see the code examples in the product package.
Performance results
To demonstrate performance, we compared Intel® MKL Sparse QR against the SuiteSparseQR [5] software package. SuiteSparseQR is based on the same multifrontal method as Intel ® MKL Sparse QR. It also uses Intel ® MKL LAPACK and BLAS functionality for computations related to frontal matrices. Execution was performed using 56 threads on an Intel Xeon® Platinum 8180 with OpenMP* threading. Several matrices from the SuiteSparse Matrix Collection (formerly known as the University of Florida Sparse Matrix Collection) were used in the comparison [6].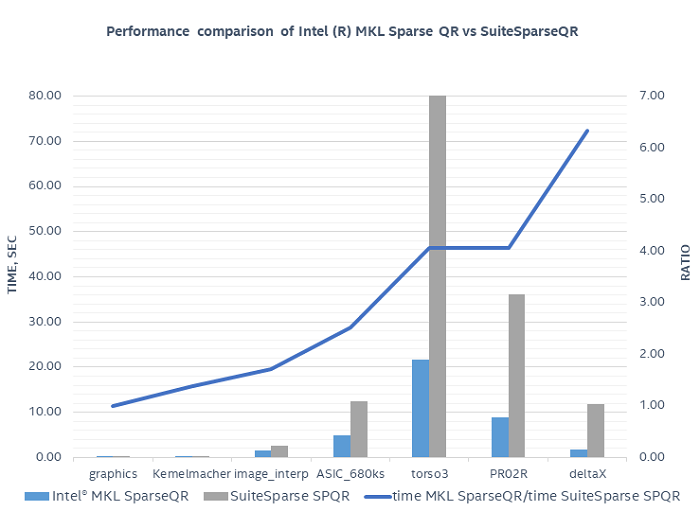
Configuration Info: Software Version: Intel® Math Kernel Library 2019; Hardware Intel(R) Xeon(R) Platinum 8180 CPU @ 2.50GHz, 2x28 Cores, 38.5 Mb L3, 192 GB DDR4 Memory,Operation System: RHEL 7.2; Benchmark: Intel Corporation.
This chart shows that Intel® MKL Sparse QR solver is faster on all tested cases with the geometric mean being 2.5x.
Additionally, both Intel ® MKL Sparse QR and SuiteSparseQR show the same accuracy in terms of relative residual with average relative residual on tested matrices being 10-10.
Contacts:
gennady.fedorov@intel.com
roman.anders@intel.com
alexander.a.kalinkin@intel.com
maria.zhukova@intel.com
References:
[1] Intel ® Math Kernel Library Sparse QR
[4] Intel ® MKL Sparse BLAS CSR Matrix Storage Format
[5] SuiteSparse: A Suite of Sparse Matrix Software
[6] SuiteSparse Matrix Collection